2-1.線形単回帰分析
最適化の考え方
単回帰は名前の通り一つ(単一)の入力xが決まれば予測値yが決まる関係が成り立つものをいいます。例えば「身長」から体重を予測するような場合で「身長」という1つ入力から「体重」を推定するというものです。ここではシンプルな線形単回帰で考え方を学習していきます。線形は直線で関係を表せ一次関数となりますので以下のような式で表せます。(a,bは定数)
$$y = ax + b$$
《参考:単回帰と重回帰》
単回帰分析と対象になるのが重回帰分析です。重回帰分析は「身長」と「体重」から肥満度を推定するような場合で「身長」と「体重」という複数の変数から求められます。以下のようにxとwが与えられるとyが得られるような式で表されます。(a,b,cは定数)
$$y = ax + bw + c$$
《参考:回帰と分類》
回帰といういうのは連続した数値、すなわち少数以下も扱う実数値を予測することをいい、分類というのは整数値を予測することになります。
では、以下に線形単回帰について説明していきます。
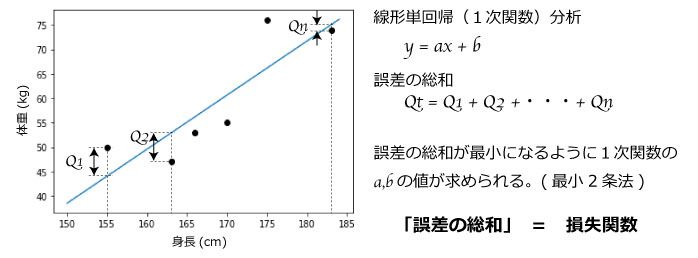
図1.一次関数と誤差の総和
図1において身長と体重を測定した点があります。実測値と予測値の各差分をQ1,Q2・・・と表すと差分の総数合計Qtは以下となります。
$$Qt = Q1 + Q2 + ・・・ + Qn$$
Qtは実測値と予測値のズレ(誤差)の総和を表すため最小になる式を導くことが最も精度良く予測した式と言えます
このQtのように実測値と予測値とのズレを損失関数または目的関数といい、最適化は損失関数が最小になるようにパラメータを調整することをいいます。
このため、線形単回帰の以下の式においてQtが最小となるa,bを求めていきます。
$$y = ax + b$$
実測値をyn、予測値(axn+b)と表すことができるため、プラスマイナス差分を同じズレとして扱うため2乗しますので誤差Qnは以下のように表せます。
$$Qn = (y_{n} – (ax_{n} + b))^{2}$$
従って各差分の総和Qtは以下となり、この総和が最小になるようにa,bを求めることで最適化することができます。(最小2乗法)
$$Qt = Q1 + Q2 + ・・・ + Qn$$
$$= (y_{1} – (ax_{1} + b))^{2} + (y_{2} – (ax_{2} + b))^{2} + ・・・ + (y_{n} – (ax_{n} + b))^{2}$$
$$= \displaystyle \sum_{i=1}^n (y_{i} – (ax_{i} + b))^{2}$$
《参考:正規方程式と勾配降下法》
上記のような最小2乗法は正規方程式を解く(数式の変形)ことで最適値を求めることができるため解析的に求めることができます。また、ニューラルネットワークのようにパラメータ数が多くあり複雑な方程式のため解くことが困難な場合があります。その場合は勾配降下法という手法を用いて数値を代入して偏微分により傾きを得ることで最小値を探していくことで最適値を得る手法を用います。勾配降下法の詳細はニューラルネットワークを参照ください。
分析プログラム
Pythonプログラムによる線形単回帰のプログラムを紹介します。プログラムと結果を簡単に見れるので「Jupyter Notebook」を利用しています。Jupyter Notebookは個人端末でも環境を構築できますが、Googleが提供しているクラウドで無料利用できる「Colaboratory」がすぐに利用できて学習目的にはオススメです。(12時間以上継続利用できないなど制限があるため実用では問題がある場合がありますが学習には問題なく利用できます)
以下はColaboratory(Jupyter Notebookでも同じです)を利用し線形単回帰モデルでデータ分析したプログラムになります。
「正規方程式」によりモデルを作成しデータを学習して最適値を出す方法と、参考に「勾配降下法」で最適値を求める手法も紹介し比較しています。


