3-1.ニューラルネットワーク(NN,DNN)
AIでは多くの手法がありますが、本ページではニューラルネットワークについて解説しています。
ニューラルネットワーク(NN)
人間の脳は神経細胞ニューロンが約100億から180億くらいあると言われており、密接に絡み合って神経のネットワークを構築しています。脳内においても個々のニューロンは入力に応じて出力のあり・なしを行っているだけのシンプルな動作ですが多数のニューロンが複雑に絡み合って動作することにより考えたり判断したり高度な処理を行っています。
人間の脳の神経細胞(ニューロン)の動きをモデル化しコンピュータで計算できるようにしたものがニューラルネットワークです。1つのニューロンをモデル化した「単純パーセプトロン」と呼ばれるものから画像識別などを行うニューラルネットワークについて仕組みを学習していきます。
1.単純パーセプトロン

図1.ニューロンと単純パーセプトロン
図1において左側がニューロン(神経細胞)をイメージしています。いくつかの入力信号があり各々の入力は強さ(シナプス*強度)が異なっています。個々のニューロンでは各入力の強さ「重み」によって出力のあり・なしが判断されています。
このニューロンをモデル化したものが図1の右側の図となります。各入力に重みをつけて合計した値が閾(しきい)値を超えるかで出力を判断しています。各入力の重みをつけた合計を「重み付き和(線形和)」といい、数式としては以下のように表すことができます。
*シナプスは他ニューロンとの接合部分のことです。
【出力なし】$$w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{3} < θ$$
【出力あり】$$w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{3} ≧ θ$$
具体的には以下の図2のようになります。

図2.単純パーセプトロンの計算(シミュレーション)例
ニューロンの動きを図2の例で説明します。各入力が「2,7,5」、重みが「0.5,0.3,0.7」となっています。各入力値に重みを掛けた値の合計(重み付き和)は6.6ですので、閾値3を超えているため「出力あり」となります。
単純パーセプトロンモデルは上記のように神経細胞ニューロンをモデル化しています。
1-1.活性化関数
ニューラルネットワークで用いる人工ニューロンモデル(以下、ニューロンモデル)は単純パーセプトロンモデルを計算しやすいように変更しています。ニューロンモデルの出力は0、1の2値ではなく任意の値も出力し利用されます。
そのため、入力に対して出力を計算するための関数を活性化関数といい閾値判定の0、1出力だけでなく多くの種類があります。活性化関数で用いる入力値は全ての入力の重み付き和から閾値を引いた「入力の線形和」と呼ばれる値を利用します。
【入力の線形和】$$w_{1}x_{1} + w_{2}x_{2} + ・・・ + w_{n}x_{n} - θ$$
図3に示す通り単純パーセプトロンは出力をあり・なし(0,1)として出力するモデルで、ある閾値を超えると1になるような関数となります。このような関数をステップ関数といい、単純パーセプトロンモデルの活性化関数はステップ関数となります。
活性化関数は多くの種類がありますが、まずは種類がある程度の理解で良いと思われます。sLab-AI学習サイトをご利用頂く場合は初期値(初期選択)のまま利用頂き、本サイトではAIの仕組み全体を大きく理解をして頂くことを目的としています。
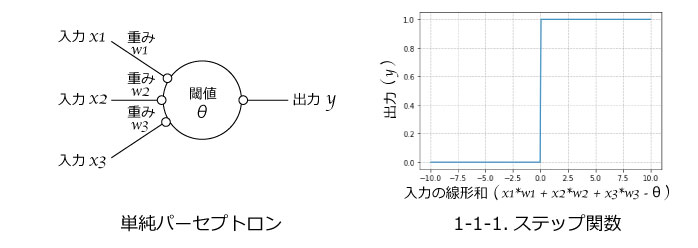
図3.単純パーセプトロンとステップ関数
複雑なニューラルネットワークではステップ関数は利用されていません。ステップ関数は微分(グラフの傾き)が使えないなど不都合な点が出てきます。そこで、各ニューロンではAI性能を向上させるべく、計算速度や確率出力など用途や目的に応じて以下のような関数が利用されています。

図4.その他の活性化関数
2.多層ニューラルネットワーク
ニューラルネットワーク(多層ニューラルネットワーク)は上記で説明したニューロンを用いて複数の階層からなるネットワークを構築して利用します。図5に入力層、中間層、出力層からなる多層ニューラルネットワークについて画像認識動作について説明します。
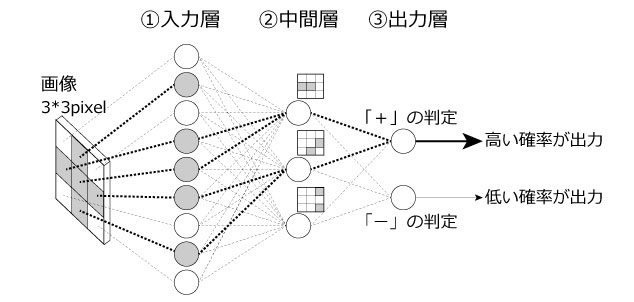
図5.多層ニューラルネットワーク
図5は3*3pixel画像の「+」と「−」を分類する多層ニューラルネットワークを示しています。各階層の役割は以下となります。
①入力層:画像情報を中間層に届ける伝搬層
②中間層:画像の特徴を抽出する層
③出力層:分類の判定を行う層
①の入力層は重みなども計算せず画像情報をそのまま中間層に渡す役割で情報を伝搬するだけの層になります。
②の中間層は画像のパターンを抽出する特徴抽出を行います。図5の太線が「重みの大きな箇所」を表し抽出している特徴パターンをニューロンの右上に表示しています。太線で示しているように重みが調整され抽出する特徴パターンがニューロン毎に調整されます。
③の出力層は分類するラベル「+」、「−」についての確率を判定する役割の層となります。
中間層と出力層のニューロンはパーセプトロンで学習した場合と同様に「重み付き和」から「活性化関数」を用いて出力を計算していきます。
2-1.AIの学習とは
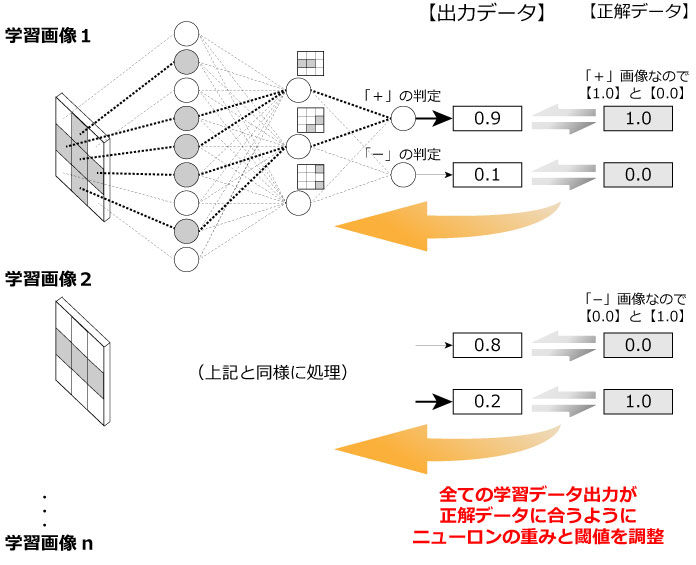
図6.ニューラルネットワークの学習イメージ
ニューラルネットワークの学習(機械学習) とは画像(入力値)に対して出力結果(ラベル)が合致するように各ニューロンの重みと閾値を調整することをいいます。
図6に「+」、「−」を識別するニューラルネットワークを例に説明します。学習前の各ニューロンにおける重みや閾値は予め決められた手法(学習前の仮値なのでランダム数値が利用される場合もあります)により仮設定されています。学習する画像の各Pixel値を入力層に入力し中間層や出力層に配置したニューロンの重みや閾値に基づいて計算し出力データを取得します。
元々の画像ラベル(正解データ)はわかっていますので、出力データと正解データを合うように中間層と出力層のニューロンの重みと閾値を調整することがニューラルネットワークの学習になります。
最初は中間層と出力層の各ニューロンの重みと閾値の初期値は仮の値で計算し、学習する画像の正解データ(ラベル)に合わせて学習の度に調整していきます。
図6のように「+」画像を入力した場合に出力データは「0.9」と「0.1」と出力されています。この場合は「+」判定するニューロンが「1(100%)」を、「−」判定するニューロンが「0(0%)」を出力するのが正解ですので出力データが正解データに近づくように【「0.9」→「1.0」、「0.1」→「0.0」】ニューロンの重みと閾値が調整されます。
また、「−」画像を入力した場合も同様に「+」判定するニューロンが「0(0%)」を、「−」判定するニューロンが「1(100%)」を出力するように【「0.8」→「0.0」、「0.2」→「1.0」】調整されます。
このように出力データの結果から入力側へ逆向きに調整を行っていくことを誤差逆伝搬法(バックプロパゲーション)といいます。
また、実際には「1」、「0」のような数値で出力させるのは困難なため、出来るだけ近い値になるようにニューロンの重みと閾値が調整されます。
1000枚の学習画像あったとしても中間層と出力層のニューロンの重みと閾値は共通ですので、全学習データに合致するようニューロンを最適化するのは容易ではないことは想像できると思います。画像データサイズが大きくなり、また学習する画像枚数も増えるとコンピュータでも多くの時間を要することになります。
2-2.損失関数(目的関数)
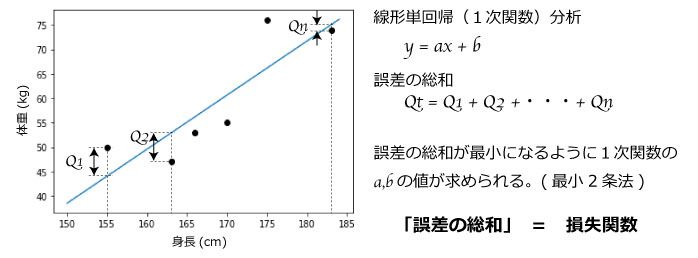
図7.線形単回帰と損失関数
損失関数を理解する上で最もシンプルな機械学習モデル(AIモデル)の線形単回帰(一次関数)で説明します。図7のように推定値(直線)と実体値(黒点)との差分Qがあり差分の総和の関数が求めることができます。この誤差が小さいことが良いモデルなので誤差の総和が最小になるように1次関数のパラメータa,bを決定しモデル化します(最小2条法)。このように誤差の総和の関数を最小化する目的でパラメータを決定するため「目的関数」、または「損失関数」といいます。
説明したように損失関数は「正解と予測値との差分の総和」を表す指標で小さいほど正解に近く良いAIということになります。
ニューラルネットワークも同様で入力データ(画像データ等)によって得られる出力(各分類ラベルの確率)が正解ラベルとの差が損失関数になります。学習データ画像は多くの枚数がありますので、全ての入力画像に対する出力ラベルと正解ラベルの差の合計が損失関数となります。この損失関数が最小となるようにニューロンの重みと閾値を調整し学習(最適化)していきます。
また、目的関数は計算の最小化(場合によっては最大化)を目的とする関数という意味で広義となり、その1つが損失関数となります。誤差関数と損失関数は同じ意味となります。
2-3.学習率(Learning Rate)と最適化手法(Optimization Method)

図8.学習率
AIの学習(機械学習と同義)とは「損失関数が最小となるパラメータ(各ニューロンの重み、閾値)を見つけ出すこと」と説明しました。ではどのように値を見つけ出すのかというと「勾配降下法」という手法で損失関数の最小値を見つけ出します。
勾配降下法は図8で示す通り偏微分により接線の傾きを求め下がる方向にxを移動しながら最小値を見つけていきます。勾配降下法は最小2条法のように方程式の変形で最適値を求めるような解析的な方法でなく、数値を代入しながら最小値を見つけていく数値的な手法です。
例えば「3x+2=11」のような式で「x=2」を代入して見ると「3x+2」は8だからxはもう少し大きい値でというように数値を代入しながら最適な値を求めていくイメージです。
手探り的な手法ですが方程式で解析的に(式の変形で)解けなくても最適値を求めていくことが可能となります。数値を代入する方法なので次にどの程度の離れた値を代入するかを決めることができ、その程度を学習率といいます。つまり、学習率は移動させる大きさ(割合)を意味しています。
図8で示すような損失関数の場合は、x0付近が最小値になるのですが局所的にはx1付近にも最小値と間違うような谷があります。部分的な最小値となる谷を局所最適値とよび、真の解を大域最適解といいます。
もちろん、求めたいのは大域最適解です。学習率を小さくすると少しづつしか動かないため大域最適解を見つけるのに学習時間を要することになります。また、学習率を大きくすると谷底をうまく見つけれずに谷底付近を行ったり来たりする可能性もあります。
そのため、最初は学習率を大きくして学習の度に小さくすることで効率的に最適な値を見つけるなどの手法が考えられます。このように、学習する度に学習率を変更することで効率的にパラメータ調整を行うことを「最適化手法(Optimization Method)」と言い多くの手法があります。(下記のボックスに手法を紹介します)
個々の手法について深く理解するのは困難なためsLab-AI学習サイトをご利用頂く場合は初期値(初期選択)のまま利用頂き、まずはAI全体の仕組みを理解頂きたいと思います。
2-4.過学習
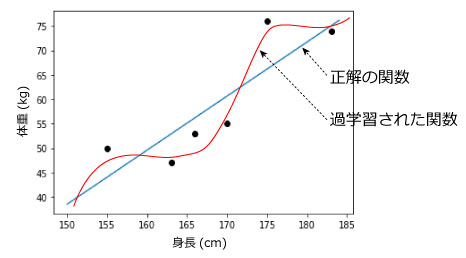
図9.過学習イメージ
学習回数(エポック*)を多くして時間をかけて学習させれば良いAIが作れるかというとそうでもありません。図9は線形単回帰(一次関数)の例となりますが本来求めたい青い直線であっても学習しすぎると赤い曲線になってしまうようなことが発生します。存在するデータに正確な値を出すのではなく、未知の値に対する予測が正確であるAIが良いAIであるはずです。また、学習データを大幅に増加させれば青い直線に近づきますので求めたいのは青い線であるはずです。しかし一部の学習データに偏って学習を実施し過ぎてしまうと赤い線のようにAI性能が悪くなることを過学習といいます。
AI学習時に学習データとは別データを用意し損失関数や正解率を確認するのは過学習とならず本来期待すべき学習しているかを検証しています。過学習とならないよう十分考慮してAI学習を行う必要があります。
*エポック(epoch)はN個の学習データ全体を反復学習すること。
3.深層学習(ディープラーニング)とディープニューラルネットワーク(DNN)

図10.ディープニューラルネットワーク(DNN)
ニューラルネットワークにおいて中間層が2つ以上の層を持つネットワークをディープニューラルネットワーク(DNN:Deep Neural Network)と言います。中間層が多くあり深く(Deep)学習できるという意味で用いられます。また、DNNを利用して機械学習を行うことを深層学習(ディープラーニング)と言います。
DNNは画像識別において非常に性能が良いことが知られており、非常に注目されている技術となります。また、畳み込みニューラルネットワーク(CNN)などもDNNの一つとなります。


